Perl Weekly Challenge: Week 281
Challenge 1:
Check Color
You are given coordinates, a string that represents the coordinates of a square of the chessboard as shown below:

Write a script to return
trueif the square islight, andfalseif the square isdark.
Example 1
Input: $coordinates = "d3"
Output: true
Example 2
Input: $coordinates = "g5"
Output: false
Example 3
Input: $coordinates = "e6"
Output: true
We can exploit the fact that the 64 squares on a chessboard strictly alternate between dark and light. If we can
convert the coordinate of a square to a number from 1 to 64, all the dark squares will be odd and the light squares
even. Actually, the range doesn't even need to be 1 to 64 to use this trick. It so happens that the .ord() method converts a character into a number—its' ASCII (or strictly speaking Unicode; ASCII is a subset of Unicode.) value. The numeric value of 'a' (and 'c', and 'e' and 'g') is odd and the numeric value of '1' (and '3' and '5', and '7') is also odd. If we add the values of the two characters in 'a1' (or 'a3' or 'c1' etc. Any dark square.) we will get an even number. Whereas any light square will give an odd number.
say @*ARGS[0].comb.map({ .ord }).sum !%% 2
So that's the solution to this problem. Split the input taken from the command-line into two characters with .comb(), convert them into numbers with .map() and .ord() and add them together with .sum(). Test that this number
is not divisble by 2 and print the result with say().
The Perl version is a bit longer because we don't have .sum() or %% and conditionals don't stringify to True and False but it is still short enough to be a one-liner.
$s; map {$s += ord} split//, shift; say $s % 2 != 1 ? "false" : "true"
Challenge 2:
Knight's Move
A Knight in chess can move from its current position to any square two rows or columns plus one column or row away. So in the diagram below, if it starts a
S, it can move to any of the squares markedE.
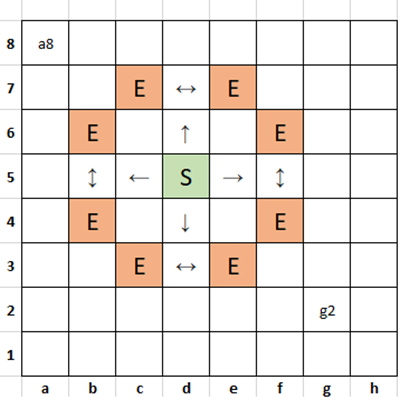
Write a script which takes a starting position and an ending position and calculates the least number of moves required.
Example 1
Input: $start = 'g2', $end = 'a8'
Ouput: 4
g2 -> e3 -> d5 -> c7 -> a8
Example 2
Input: $start = 'g2', $end = 'h2'
Ouput: 3
g2 -> e3 -> f1 -> h2
Long ago in Weekly Challenge 118 we had a similar task. I solved it using the IDA* algorithm and I've reused that code for this problem with a few changes to make the code more generic and correcting some bugs I noticed. It's probably overkill for this particular problem but I didn't feel like writing a new solution from scratch.
We need to represent squares on the chessboard which is what this class does.
class Position {
It has data members that represent the row and the column of the square as numbers.
has Int $.row is rw;
has Int $.col is rw;
The constructor is overidden to use positional arguments instead of named arguments which are the default in Raku.
method new( $row, $col ) {
self.bless(:$row, :$col);
}
The .Str() method is also overidden so when we print a Position it will
be displayed in chess algebraic notation.
method Str {
('a'.ord + $!col).chr ~ (8 - $!row).Str;
}
}
We will also need to compare if two Positions are equal. This is achieved by overloading operator <=>.
multi sub infix:<==>(Position $a, Position $b) returns Bool {
return $a.row == $b.row && $a.col == $b.col;
}
Lets turn to the MAIN() subroutine before proceeding further.
The main (haha!) thing it does is take two chessboard positions in algebraic notation from the command-line
arguments and uses them to create two Position objects, $start and $end.
my ($sc, $sr) = $s.comb;
my ($ec, $er) = $e.comb;
Like in task 1, the conversion is made using .ord(). It's a little more complicated than it could be
because, my IDA* code assumes the origin (the 0,0 co-ordinate) is in the top-left corner whereas on a chessboard
it is actually the bottom-left. I don't remember exactly why I did this. I think it might have been because my
original c++ IDA* implementation did it that way.
my $start = Position.new('8'.ord - $sr.ord, $sc.ord - 'a'.ord );
my $end = Position.new('8'.ord - $er.ord, $ec.ord - 'a'.ord);
The makePath() function (to be described below.) will return a list of Positions which represent the shortest
possible path from $start to $end inclusive. We count the length of that path with .elems(). Because the spec doesn't want us to include $start, we have to subtract 1 from that length before printing it.
say makePath($start, $end).elems - 1;
This is makePath(). It will repeatedly call search() to find paths until the shortest has been found.
sub makePath(Position $start, Position $end) {
my Position @path = [ $start ];
my $bound = estimatedCost($start, $end);
loop {
my $t = search(@path, $end, 0, $bound);
if $t ~~ -∞ {
last;
}
# Can't solve; this shouldn't happen.
if $t ~~ ∞ {
last;
}
$estimate = $t;
}
return @path;
}
search() takes the path developed so far, the target position, the cost of the path so far
and the estimated upper bound of how high this cost should go.
sub search(Position @path, Position $target, Int $cost, Int $bound) {
my $current = @path[*-1];
It determines the cost of extending the path one more step using estimatedCost().
my $estimate = $cost + estimatedCost($current, $target);
If the estimate was greater than the upper bound, this is not the shortest path so we stop searching and return the estimate which will become the new upper bound.
if $estimate > $bound {
return $estimate;
}
If we are already at the target, we return the lowest possible estimate, negative infinity.
if $current == $target {
return -∞;
}
Otherwise, a variable is set up for the minimum estimated cost of the path. It is initially set to the highest possible value, infinity.
my $min = ∞;
for each possible move from the current position given to us by the possibleMoves() function...
for possibleMoves($current, $target) -> $move {
...if it isn't already on the path (to prevent going round in circles)...
if $move ⊄ @path {
...it is added to the path and search() is recursively called again. The $estimate argument to this function
is proved by adding the result of stepCost() to the current cost.
@path.push($move);
my $t = search(@path, $target, $cost + stepCost($move), $bound);
If a previoussearch() had returned negative infinity, it is propogsted to the return value of this instance
and so on until the recursion is unwound and search() returns altogether.
if $t == -∞ {
return -∞;
}
If the estimate returned by the previous search() is less than our current minimum estimate, it becomes
the new minimum.
if $t < $min {
$min = $t;
}
The current move is removed from the path so the next possible move can be tried.
@path.pop;
}
}
After all possible moves have been tried, th
return $min;
}
In order to find the shortest path we have to know if the move we are contemplating will bring
us nearer or further from the goal. The "cost" of the move may vary. For instance in a wargame, going through
three mountain spaces might take longer than seven paved road spaces even though the former seems to be closer.
Thus the estimatedCost() function provides an idea of what the cost may be. However on a chessboard, all squares
are equally accessible to the knight so our implementation just returns 1.
sub estimatedCost(Position $position, Position $goal) {
return 1;
}
The stepCost() function gives the actual cost of moving to the next square. As this is also the same for
every square on the chessboard, it also only returns 1.
sub stepCost(Position $position) {
return 1;
}
The possibleMoves() function returns a list of the next moves the knight can make from its' current position.
It uses tryMove() to ensure a possible move doesn't go off the board.
sub possibleMoves(Position $position, Position $target) {
state @deltas = [
Position.new(-2, -1),
Position.new(-2, 1),
Position.new(-1, 2),
Position.new(1, 2),
Position.new(2, 1),
Position.new(2, -1),
Position.new(-1, -2),
Position.new(1, -2)
];
my @moves;
for @deltas -> $delta {
my $move = tryMove($position, $delta);
if $move {
@moves.push($move);
}
}
In most scenarios where IDA* is used, it is more efficient to select the next move with the lowest estimated cost first (even though thst may not actually turn out to be the optimal one.) In this case, because moving to any square has the same cost, this sort is redundant. I didn't bother taking it out though because it didn't have much of an impact on performance.
@moves = @moves.sort({
estimatedCost($^a, $target) < estimatedCost($^b, $target);
});
return @moves;
}
sub tryMove(Position $position, Position $delta) {
my $dest = $position.clone;
$dest.row += $delta.row;
$dest.col += $delta.col;
return ($dest.row >= 0 && $dest.row < 8 && $dest.col >= 0 && $dest.col < 8)
?? $dest
!! Nil;
}
This is the Perl version. For the Position class, I used Moo.
I need to try out the new in-core Perl object system one of these days but I'm still on version 5.38 for now.
package Position;
use Moo;
use namespace::clean;
use overload '==' => \&compare;
has row => (
is => 'rw',
);
has col => (
is => 'rw',
);
around BUILDARGS => sub($orig, $class, @args) {
return { row => $args[0], col => $args[1] };
};
sub str {
my ($self) = @_;
return chr(ord('a') + $self->col) . (8 - $self->row);
}
sub compare {
my ($self, $other) = @_;
return $self->row == $other->row && $self->col == $other->col;
}
1;
The rest of the code follows the Raku implementation.
package main;
sub estimatedCost {
return 1;
}
sub stepCost($position) {
return 1;
}
sub tryMove($position, $delta) {
my $dest = Position->new($position->row + $delta->row, $position->col + $delta->col);
return ($dest->row >= 0 && $dest->row < 8 && $dest->col >= 0 && $dest->col < 8)
? $dest
: undef;
}
sub possibleMoves($position, $target) {
state @deltas = (
Position->new(-2, -1),
Position->new(-2, 1),
Position->new(-1, 2),
Position->new(1, 2),
Position->new(2, 1),
Position->new(2, -1),
Position->new(-1, -2),
Position->new(1, -2)
);
my @moves;
for my $delta (@deltas) {
my $move = tryMove($position, $delta);
if (defined $move) {
push @moves, $move;
}
}
@moves = sort { estimatedCost($a, $target) < estimatedCost($b, $target); } @moves;
return @moves;
}
sub search($path, $target, $cost, $bound) {
my $current = $path->[-1];
my $estimate = $cost + estimatedCost($current, $target);
if ($estimate > $bound) {
return $estimate;
}
if ($current == $target) {
return '-inf';
}
my $min = 'inf';
for my $move (possibleMoves($current, $target)) {
if (!grep { $_ == $move } @{$path}) {
push @{$path}, $move;
my $t = search($path, $target, $cost + stepCost($move), $bound);
if ($t == '-inf') {
return '-inf';
}
if ($t < $min) {
$min = $t;
}
pop @{$path};
}
}
return $min;
}
sub makePath($current, $target) {
my @path = ( $current );
my $bound = estimatedCost($current, $target);
while(1) {
my $t = search(\@path, $target, 0, $bound);
if ($t == '-inf') {
last;
}
# Can't solve; this shouldn't happen.
if ($t == 'inf') {
last;
}
$bound = $t;
}
return @path;
}
my ($sc, $sr) = split //, shift;
my ($ec, $er) = split //, shift;
my $start = Position->new(ord('8') - ord($sr), ord($sc) - ord('a'));
my $end = Position->new(ord('8') - ord($er), ord($ec) - ord('a'));
say scalar makePath($start, $end) - 1;